The Joy (and importance of) of Mistake-Making

The longer I teach, the more I am struck by what happens in the first few weeks of school. There is so much purpose layered into those first moments together, be it in classes, time in community, in advisory, out at recess. When I think back to my first year teaching math (I was teaching high school Algebra 2 and Geometry), I was eager to dive in to the curriculum and to avoid all the messy stuff that comes with new beginnings, new faces, new feelings. Now in my seventeenth year of teaching (and most of that at the middle school level), I know full well that we must spend time crafting the culture of our classrooms at the outset of the year. That culture comes from mindfully, purposefully, explicitly laying out what we want learning to look like.

One of the most important pieces of math culture I want to encourage is collaboration and sharing one's thinking. That means being willing to take risks and share ideas that may be wrong, so we need to be comfortable talking about our mistakes. Without explicitly teaching that, I realized that in subtle ways, this message of being comfortable making mistakes has permeated so much of my early lesson plans and collaborative work across grades 6 through 8. And just two weeks into school, I have witnessed several moments of downright joy in mistake-making.

My 8th graders have been with me the longest - most of them are starting their third year with me. They are steeped in the culture of mistake-making, but I am still blown away by their non-attachment to mistakes, their willingness to dive back in after a setback. In their first encounter with Desmos activities last week, students worked on creating graphs that precisely matched the rate of filling of different glasses:

gif courtesy of Desmos

But then, they got to create their own glasses, graph the rates of filling, and challenge their classmates to try their glasses. And what they made for one another was WAY more challenging than the original activity:

And they were super excited to try one another's creations, even if it meant going back over and over again to revise and refine their matching graphs.  Their tenacity in attending to precision was astounding. You could have heard a pin drop in the room as kids were poised over their computers. And there were several instances of joyful jazz hands when they were able to achieve the ranking of "very precise."

In 7th grade, students are doing corrections from their end of year quiz last year. Many of them are looking at the question that asked them to find the volume of a trapezoidal prism and wondering why they multiplied l*w*h. This is a powerful misconception that must be unlearned and reinforced with cognitive dissonance though problems like these. And while it may be a strong statement to say their corrections bring them joy, they are certainly satisfied with themselves for completing a complex problem like this, comprised of many sub-problems.

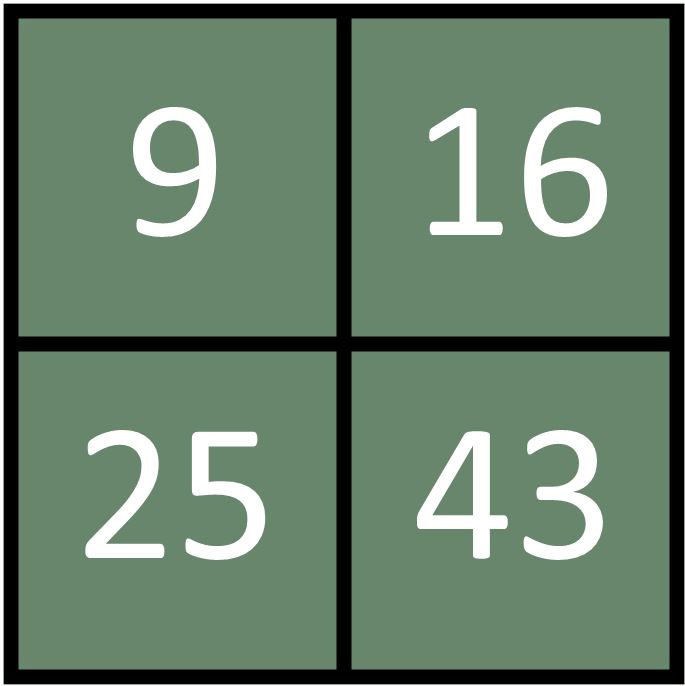
In 6th grade, my newest students have impressed me right out of the gate with their willingness to engage in debate over the "right" answer. During a "Which One Doesn't Belong" activity (where students find ways that each number may not belong), they stated that 16 in the following image doesn't belong because it is the only one with an odd tens digit.

image from wodb.ca

There was then a very involved debate about whether 0 was even, odd, or neither, with many arguments formed on either side. 

Later that week, we did the Four 4's activity and someone put up the following expression that equalled 5:  

As we closed class, I put it up on the board and asked the class what they thought it equalled. There were 2 answers: 5 or 17. Again, both sides weighed in and we talked about order of operations which settled it for 17.

In both of the cases with 6th grade, I assured them that even math teachers have trouble with these types of questions. My mentor teacher Henri used the term "mathematical consensus" to describe how we as a community of mathematicians have decided to agree upon such "right" answers, and I love this term. It makes math a dynamic subject, one where logical arguments are vetted together rather than answers handed down from the holy textbook on high.

As we embark on another year of messiness (in the best way) in middle school, I also must take a moment to pay homage to those teachers that have come before me, laying the groundwork for kids to feel safe taking risks, to feel valued for their deep thinking rather than their speed of computation, to have the courage to question things we seem to tacitly accept, to know that mistakes are part of the learning process. For beyond each mistake, each frustration, each wrong solution path lies the aha moment. The joy in that is audible, palpable, contagious. Which why I love teaching middle school.